Definitions of Graph
Graph
A graph G = (V,E) consists of
- a set V of vertices(nodes)
- a collection E of pairs of vertices(nodes) from V called edges(arcs)
Example of Graph:
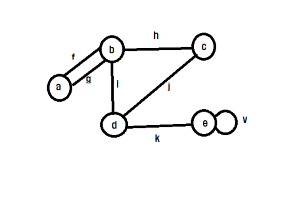vertices = V : [a,b,c,d,e]
edges = E : [[a,b],[a,b],[b,c], [b,d], [c,d], [d,e],[e,e]] or [f,g,h,i,j,k,v]
Undirected Edges
An undirected edge h represents a symmetric relationship between vertices b and c. In ohter words, edge h has both directions between vertices b and c.
- We can represent h = [b,c], where [b,c] is an unordered pair
- b and c are the endpoints of the edge
- b is adjacent to c
- h is incident to b and c
- The degree of a vertex is the number of incident edges
e.g. deg(b) = 4, deg(e) = 3 - Parallel edges(multi-edges): more than one edge between pairs of vertices
- Self-loop: edge that connects a vertex to itself(e.g. e)
Undirected Paths
A walk in a graph is a sequence of vertices $v_1,v_2,v_3,…,v_k$, such that there exist edges $[v_1,v_2],[v_2,v_3],…,[v_{k-1},v_k]$
- The length of a walk is the number of edges.
- If $v_1=v_k$, the walk is closed. Otherwise, it is open.
- If no edge is repeated, it is a trail.
- A closed trail is is a circuit.
- Path: no vertex is repeated.
- Cycle: a path with the same start and ed vertices
Connected Graphs
connected graph : every pair of vertices is connected by a path
ex)
- Connected graph
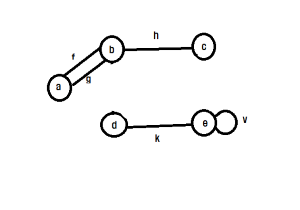
- Disconnected graph
- Two connected components
Simple Graphs
A simple graph is a graph with no self-loops and no parallel / multi-edges
- Theorem: $\sum_{v \in V}deg(v)=2m$, where m stands for number of edge, and v stands for a vertex.
- Theorem: Let G be a simple graph with n vertices and m edges, Then, $m \le \frac {n(n-1)} {2}$
- Corollary: A simple graph with n vertices has $O(n^2)$ edges
Complete Graphs
Complete graph: simple graph where every pair of vertices is connected by an edge
- The complete graph on n vertices has exactly $\frac{n(n-1)}{2}$ edges
- The complete graph on n vertices with one self-loop per vertex has exactly $\frac{n(n+1)}{2}$ edges
Subgraphs
A subgraph of G = (V,E) is a graph G’ = (V’, E’) where
- $V’\subseteq V$
- E’ consists of edges [u,v] in E such that both u and v are in V’
A spanning subgraph G’ of G contains all vertices of G
An induced subgraph G’ of G contains all the edges of G that have both endpoints in G’
Trees and Forests
A (free)tree is an undirected graph T such that
- T is connected
- T has no cycles
A rooted tree is a trees where one vertex is designated as the root
Forest: undirected graph without cycles(collection of disconnected trees)
- The connected components of a forest are trees
Spanning Trees and Forests
A spanning tree of a connected graph is a spanning subgraph that is a tree
- A spanning tree is not unique unless the graph is tree
A spanning forest of a graph is a spanning subgraph that is a forest(e.g. disconnected subgraph that has all vertices)
Properties of Graphs, Trees, and Forests
Theorem: Let G be an undirected simple graph with n vertices and m edges. Then have the following:
- If G is connected, then $m \ge {n-1}$
- If G is a tree, then $m=n-1$
- If G is a forest, then $m \le n-1$
Graph Representation
Let G is graph that is n vertices and m edges…
Set of Edges
A set of edges is collection of edges.
- Note that some vertices have to store sperately, since some might have not edges.
Adjacency Matrix
Maintain a 2-dimensional n x n boolean array.
For each edge [u,v], G[u][v]=G[v][u]= true(1).
Adjacency matrix takes $O(n^2)$ space.
Adjacency List
Maintain an array indexed by vertices which points to a list of adjacent verices.
Adjacency list takes $O(n+m)$ space.
Number of Possible Spanning Subgraphs
Since all verices must be included in the subgraph, we only have a choice about which edges to include. It has same behavior of number of subset.
With m edges, $2^m$ possibilities for spanning subgraph.
Number of Possible Induced Subgraphs
All edges must be included between the vertices we choose.
With n vertices, $2^n$ possibilities for induced subgraph.